| 니앙팽이 - 자료구조| 3 | 트리, 이진트리 노트

트리

트리의 구성 요소

❗ 기본 트리의 구성 요소

• 노드
• 간선
  • 노드와 노드를 연결하는선
• 서브 트리
  • 트리를 구성하는 작은 트리
  • 트리는 재귀적이다.

❗ 관점에 따른 노드 분류

• 👉 위치에 대한 관점
• 루트 노드
  ■ 맨 꼭데기 노드
• 단말 노드
  ■ 자식이 없는 노드
• 내부 노드
  ■ 단말 노드 이외 노드

• 👉 상위, 하위 관점
• 부모 노드
  ■ 자식을 가지고 있는노드
• 자식 노드
  ■ 부모가 있는 노드
• 형제 노드
  ■ 부모가 있고 Depth가 동일한 노드

트리의 분류

❗ depth / level

• 트리의 깊이혹은 높이라 부른다
• 어떤 트리의 depth / level을 물어볼때 최대 depth를 말하면 된다.
• 가족관계
  • 현재 노드 : i;
  • 부모 : i/2;
  • 왼쪽 : 2i;
  • 오른쪽 : 2i + 1;

👉 이진 트리

• 노드 하나를 중심으로 2개의 서브트리로 나뉘어 지는 트리
• 공집합도 이진트리로 포함해야한다.

1	2

👉 완전 이진 트리

• 노드가 좌측부터 채워지는 이진 트리
• 구현
  • 배열로 이진트리를 만들수 있다.
    • 인덱스 순차 증가접근은 depth 순서로 접근하는것이다.

• #include <iostream>
  using namespace std;
  int comTree[10101];
  
  int GetPar(int _cur){
    return _cur / 2;
  }
  int GetLeft(int _cur){
    return _cur * 2;
  }
  int GetRight(int _cur){
    return _cur * 2 + 1;
  }
  
  int main(){
    int N; cin >> N;
    for(int i = 1; i <= N; i++){
      cin >> comTree[i];   
    } 
  }
  

👉 포화 이진 트리

• depth에 대해 꽉찬 이진 트리

---

트리의 운행법

• preorder : M, L, R

• inorder : L, M, R

  • 이진탐색트리에서 중위순회를 하면
  • 오름차순으로 정렬된 순서로 Key를 가져올 수 있음

• postorder : L, R, M

❗ 명칭

• 연산자

  +, -, *, /...

• 피연산자

  A, B, C ...

❗ 수식연산 알고리즘

👉 1. 전위표기법 (EX. +AB)

• preorder : M, L, R
• 연산자를 먼저 표시하고 연산에 필요한
  피연산자를 나중에 표기하는 방법

👉 2. 중위 표기법 (EX. A+B)

• inorder : L, M, R
• 연산자를 두 피연산자 사이에 표기하는 방법으로
  가장 일반적으로 사용되는 방법

👉 3. 후위 표기법 (EX. AB+)

• postorder : L, R, M
• 피연산자를 먼저 표시하고 연산자를
  나중에 표시하는 방법

이진 탐색트리

https://gist.github.com/harish-r/a7df7ce576dda35c9660

• 

문제점

• 위 두 트리는 각각 이진 탐색 트리가 맞는데..
  • 우측은 Skewed 이진 탐색트리라고 한다..
  • 근데 이렇게 배치되면 사실상 연결리스트랑 다를바가 없다. (비효율)
    • 왜 이런일이 생기냐.. 연달아 큰것들이 들어와서 저렇다
    • 만약 들어오는 순서가 달랐다면 다른 모양이 되었겠지..
      • 인풋 순서에 따라 결정된다.
    • 이것을 해결하기위해 ( 레드블랙트리 ) 사용한다.

정의

❗ 이진 트리 기반 자료구조다

• 단 완전 이진트리 형식은 아닐수도 있다
• 들어온 노드에 따라 형태가 배뀌기 떄문이다

❗ 노드간 특징

• L < M < R

동작

탐색

• 찾으려는값 < 현재 서브트리의 루트
  • 왼쪽 서브트리로 간다.

삽입

• 각 레벨마다 왼쪽 혹은 오른쪽 서브트리를 선택하면서 쭉쭉 내려오다가
• leaf노드에 도달하면 멈추기

삭제

• 삭제 케이스는 노드 자식에 따라 다르다
  1. 삭제 노드의 서브트리가 0개
  2. 삭제 노드의 서브트리가 1개
  3. 삭제 노드의 서브트리가 2개

이진 탐색 트리코드 - <클릭>

힙

힙의 구성 요소

❗ 힙 정의

👉 완전 이진트리 기반 자료구조

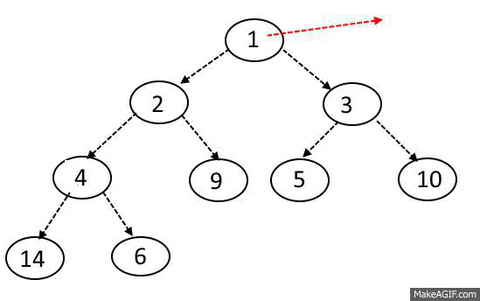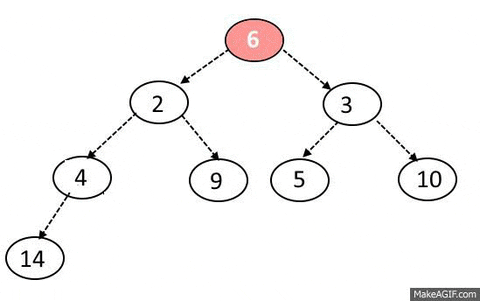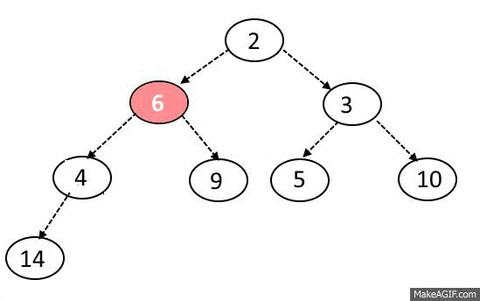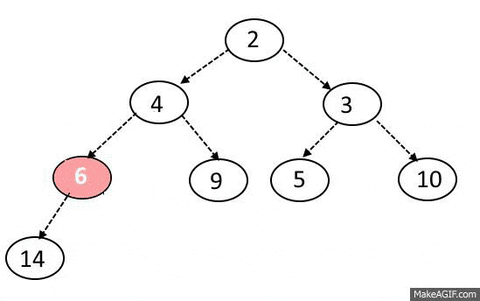
• 최댓값 및 최솟값을 찾아내는 연산을 빠르게 하기위해 고안된 자료구조다
  • 완전 이진트리를 기본으로 한 자료구조다

👉 노드간 특징

• 부모 노드는 항상 자식노드 값사이 대소관계가 존재한다.
• 단, 형제 노드사이에는 대소관계를 모른다.

👉 배열 VS 힙 (극값 탐색 시간)

___	배열	힙
삽입삭제	O(1),O(N)	O(lg), O(lg)
극값탐색	O(N)	O(1)

❗ 힙 종류

https://gist.github.com/jmkim/1920a4ff2ac3cb0252d6a76f3c8d97cc

👉 Min-Heap	👉Max-Heap
부모노드의 키값이 자식노드의 키값보다 항상 큰 힙 데이터를 모두 양수라고 하면 max 힙	부모노드의 키값이 자식노드의 키값보다 항상 작은 힙 데이터를 모두 음수 치환하면 min 힙

힙의 동작

insert	delete
O(log N)	O(log N)

코드에서 사용하려면...

#include <queue>
struct comp{
    bool operator()(자료형 &A, 자료형 &B){
        return A.--- < B.---;//max힙
        return A.--- > B.---;//min힙
    }
}
                :
                :
                :
    
priority_queue<자료형, vector<자료형>, comp 함수>

/*
comp 함수는 일반적인 정렬 방식과 
반대 양상이 나타난다;;; 
*/

레드 블랙 트리

레드블랙 트리 블로그

개요

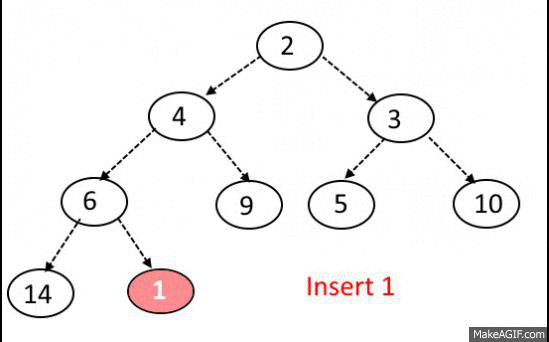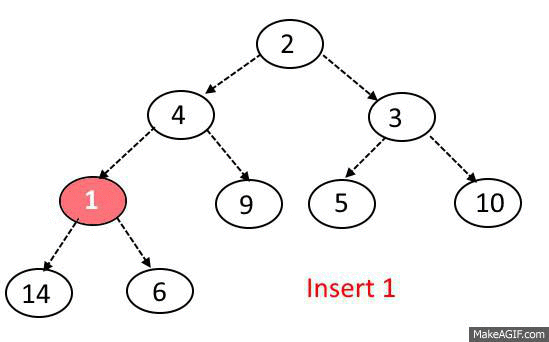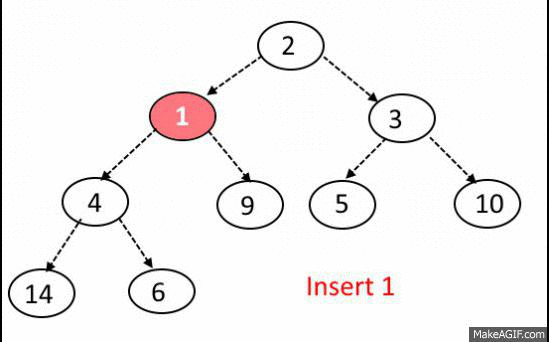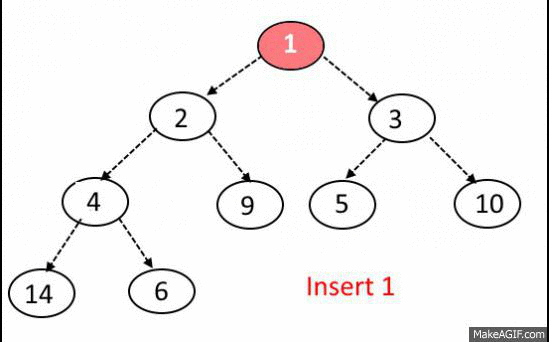
이진 탐색 트리의 삽입, 삭제 연산과정에서 발생되는 문제를 해결하고자 나온 트리이다
기본은 BST 이지만 동일한 노드의 개수일 때, depth를 최소화 하여
Search, Insert, Delete 시간복잡도가 O(logn)소요 된다.

이진 탐색 트리와 다른것이 또 있다면 완전 이진 트리라는 점이다.

정의

1. 각 노드는 Red or Black 이다
2. 루트노드 단말노드는 모드 블랙이다.
3. 레드의 자식은 블랙이다

특징

1. BST의 특징을 모두갖는다